Deriving an Optimally Tuned PID Controller for Precise DC Motor Velocity Control

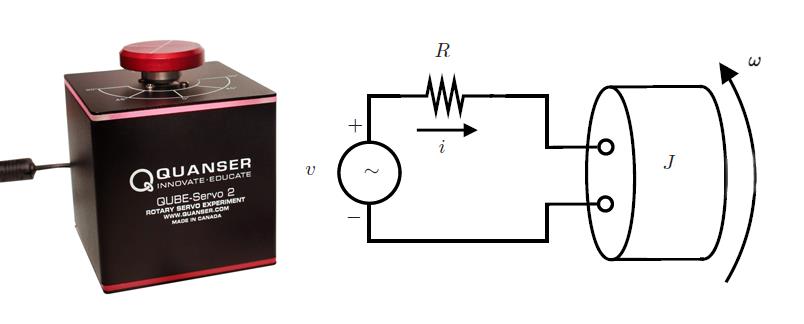
The problem of velocity control of a DC motor is a canonical toy problem for testing new controllers. Velocity control of DC motors has a wide range of applications, from garage door openers to robots. We optimized a Proportional-Integral-Derivative (PID) controller for the velocity control of a DC motor in the Quanser QUBE-Servo 2 system. The objective was to determine the optimal values of the PID parameters (proportional gain \(k_p\), integral gain \(k_i\), and derivative gain \(k_d\)) that minimize the integral squared error (ISE) of the closed-loop system, while satisfying constraints like nonnegativity of the PID parameters and actuation limits. MATLAB’s fmincon function was used to solve the optimization problem.

The Quanser QUBE-Servo 2 is a rotary servo system featuring a direct-drive 18-volt brushed DC motor. The motor is modeled using the following system of equations:

\[ iR + K_g \omega = v(t) \]

\[ J \dot{\omega} = K_m i \]

Where:

• \(v(t)\) is the voltage source,
• \(R\) is the motor armature,
• \(K_g\) and \(K_m\) are the back emf and motor torque constants,
• \(i\) is the current,
• \(J\) is the combined mass moment of inertia,
• \(\omega\) is the angular velocity of the shaft.

The transfer function between the input voltage \(v\) and output angular velocity \(\omega\) is:

\[ P(s) = \frac{\Omega}{V} = \frac{23.8}{0.1s + 1} \]

The goal of this project is to design a PID controller to improve the response of the motor to changes in input. The controller structure in the \(s\)-domain is:

\[ U = \left(k_p + \frac{k_i}{s} + k_d s \right) E \]

Due to practical constraints, the derivative term is replaced by a “dirty derivative” to avoid issues with noise:

\[ k_d s \approx k_d \frac{s}{\sigma s + 1} \]

The optimization objective is to minimize the ISE for the closed-loop system with the PID controller. The ISE is calculated as:

\[ \text{ISE} = \int_0^\infty e(t)^2 dt \]

Where \(e(t) = 1 - y(t)\), the difference between the step input and system output. The PID parameters are subject to constraints:

• \(k_p, k_i, k_d \geq 0\),
• \(k_p, k_i, k_d \leq 10\),
• \(k_p + k_i + k_d \leq 15\).

The optimization problem is solved using MATLAB’s fmincon function.