Implementation of Operational Space Control Barrier Functions on Franka Manipulator

Together with Mateusz Jaszczuk, I implemented a safety-critical control framework that integrates control barrier functions (CBFs) into an operational space controller for a 7-DoF Franka Emika Panda manipulator. The goal of the project was to enforce joint limits, obstacle avoidance, and self-collision avoidance in real time while preserving the behavior of a nominal Cartesian impedance controller. The system was evaluated in simulation on tasks that would normally result in collisions, demonstrating that safety constraints can be enforced reliably at control-loop rates suitable for hardware deployment.
The controller was implemented in Python using PyBullet for dynamics and OSQP for real-time quadratic programming, and achieved sustained loop rates on the order of 1 kHz in headless mode.
Control Architecture
The baseline controller follows a standard operational space formulation, generating Cartesian forces to track desired end-effector velocities and mapping them into joint torques through the Jacobian transpose. Rather than modifying this controller directly, we treated its output as a nominal torque command and wrapped it in an instantaneous quadratic program.
At each control step, the QP computes the closest feasible torque to the nominal command while satisfying a set of linear inequality constraints derived from control barrier functions. This formulation allows safety constraints to intervene only when necessary, leaving task execution largely unchanged in unconstrained regions of the state space.
Safety Constraints via CBFs
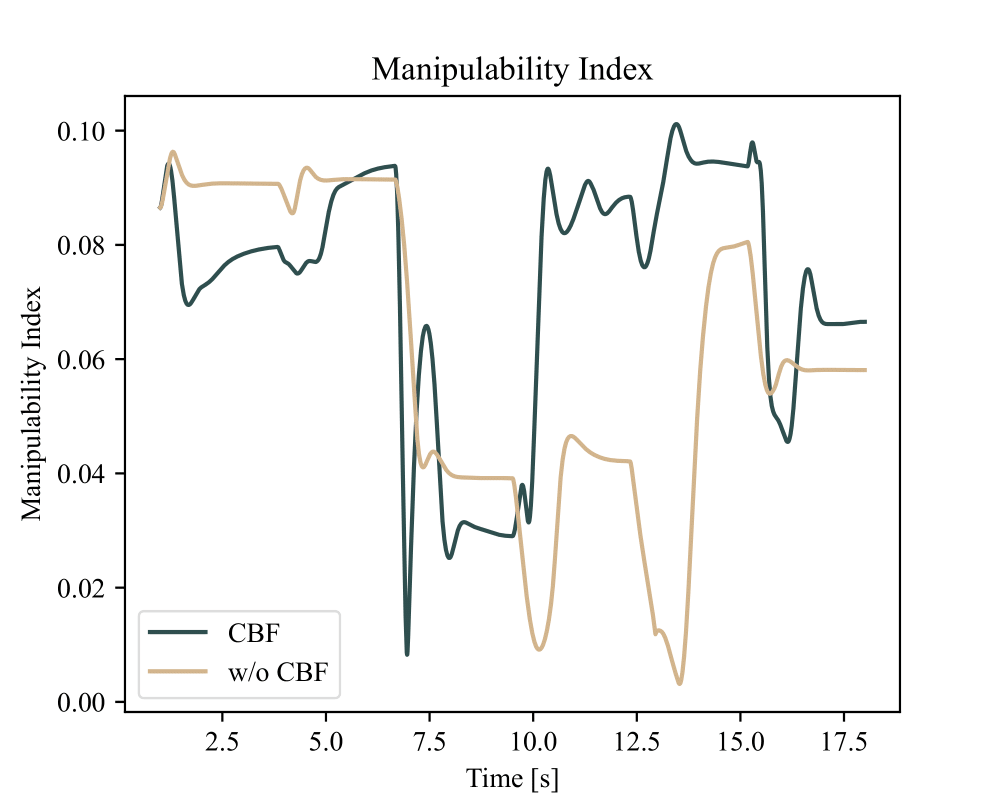
We implemented three classes of safety constraints. Joint limit avoidance was enforced using a pair of barrier functions per joint, preventing motion toward either limit. Obstacle avoidance was handled by modeling both the robot and external obstacles as collections of spheres and enforcing separation constraints between them. Self-collision avoidance was implemented similarly, constraining the distance between internal robot body spheres and the end effector.
Because these constraints depend only on configuration, they have relative degree two with respect to the torque input. To handle this, we used high-order control barrier functions, enforcing second-order conditions that ensure forward invariance of the safe set under the full manipulator dynamics. This required explicit use of the mass matrix, Coriolis terms, gravity, and Jacobians at each control step.
Real-Time Implementation
Achieving real-time performance required careful attention to implementation details. All QP matrices were preallocated with fixed sparsity patterns, and only their numerical values were updated online. This allowed the solver to reuse factorization structure across iterations, avoiding costly reallocations.
Dynamics quantities were queried directly from PyBullet at each timestep, with the inverse mass matrix computed once per loop and reused across all barrier evaluations. With this setup, the full controller including joint limits, self-collision, and obstacle avoidance consistently ran at approximately 1.3 kHz in headless simulation, satisfying the timing requirements of the Franka platform.
Evaluation
To evaluate the controller, we designed a sequence of Cartesian targets that deliberately induced unsafe behavior under the nominal controller. One trajectory passed directly through an external obstacle, while another caused the end effector to collide with the robot’s own links.
With the CBF constraints active, the controller generated smooth, collision-free trajectories in both cases. Barrier function values remained nonnegative throughout execution, indicating that safety was maintained despite discretization and modeling error.
Manipulability-Aware Null-Space Control
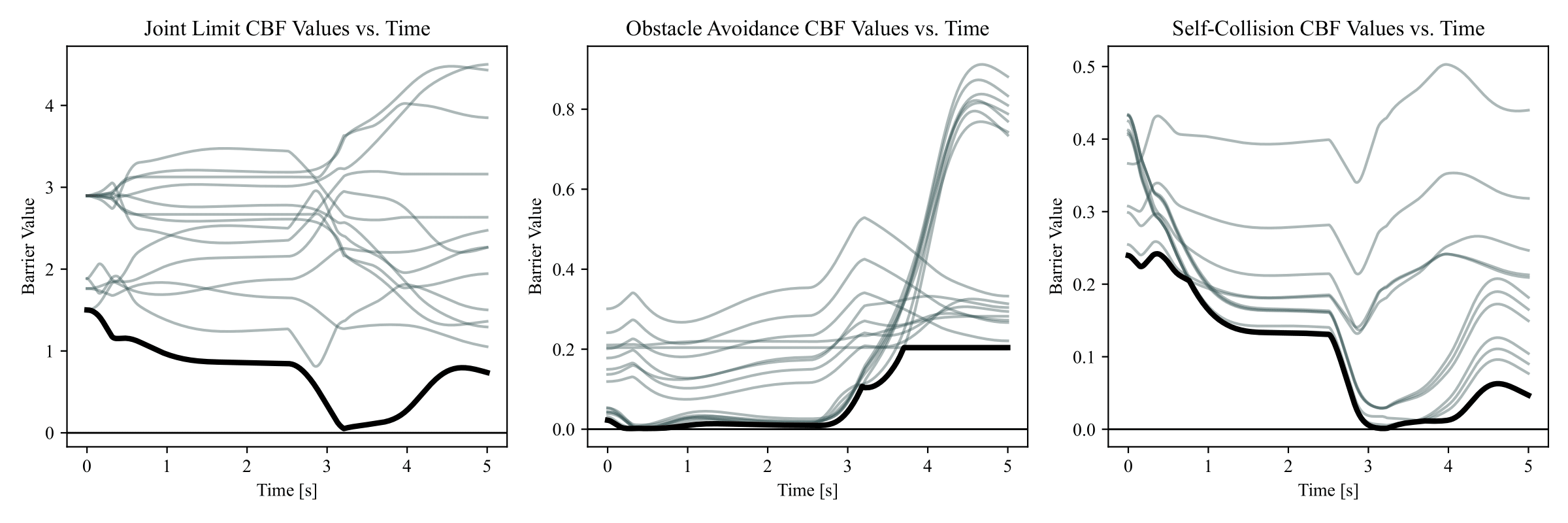
In addition to hard safety constraints, we explored a soft CBF formulation for manipulability maximization. Using an IKFlow-based sampler, we identified high-manipulability joint configurations for a given end-effector pose and introduced a slackened barrier that gently biased the controller toward these configurations.
This objective was evaluated separately from the real-time controller, as it is not safety-critical. Results showed that soft CBFs can effectively shape null-space behavior without interfering with task-space tracking, suggesting a flexible mechanism for incorporating secondary objectives into constrained controllers.