Performance Analysis of Boids for Coverage
This work, conducted in collaboration with Jason Chen, investigates the use of Reynolds-style boids as a distributed coverage algorithm. We formalized the canonical separation, alignment, and cohesion rules in terms of repulsive and attractive control forces, implemented a custom high-throughput simulator, and performed large-scale parameter sweeps to quantify coverage efficiency and uniformity across heterogeneous environments. The analysis emphasizes the tradeoffs inherent in minimal local coordination and identifies gain regimes that maximize exploration under geometric constraints.

Simulation Framework
Agents are modeled as kinematic point masses with bounded acceleration. Each agent executes a prioritized behavior stack at every timestep: obstacle avoidance, wall repulsion, separation, alignment, cohesion, and (optionally) target seeking. The prioritization ensures that collision-avoidance consumes control authority before lower-priority objectives, rather than relying on naive vector summation. Local sensing is restricted to a fixed radius and field of view.
The governing interaction terms are:
Separation
\[f_{\text{sep}} = k_{\text{sep}} \sum_{j \in \mathcal{N}_i} (x_i - x_j)\]Alignment
\[f_{\text{ali}} = k_{\text{ali}} \left( \frac{1}{|\mathcal{N}_i|} \sum_{j \in \mathcal{N}_i} \dot{x}_j - \dot{x}_i \right)\]Cohesion
\[f_{\text{coh}} = k_{\text{coh}} \left( \frac{1}{|\mathcal{N}_i|} \sum_{j \in \mathcal{N}_i} x_j - x_i \right)\]
Obstacle and wall repulsion are modeled with smooth inverse-distance fields. The net control input is clipped to a maximum magnitude per step.
The simulator, implemented in Python/PyGame, provides both interactive mode (for manual tuning and visualization) and headless mode (for batched experiments). Trials run at 60 Hz over 60 s in domains discretized at 800×600 resolution. Headless mode supports 100+ simultaneous runs with seeded randomization to ensure statistical validity.
Coverage Task and Metrics
The primary objective is spatial coverage: maximizing the fraction of free workspace area visited at least once by any agent. A binary coverage mask is updated each frame by inflating agent positions by a small footprint radius. To measure efficiency of exploration, we also compute the coefficient of variation (CV) of visit counts per pixel. High coverage with low CV corresponds to rapid and uniform exploration; high coverage with high CV indicates redundant retracing.
The benchmark set contains four environments with different constraints: a dense cafeteria layout, a standard cafeteria, a narrow corridor with a bottleneck, and an empty arena. These span heavy clutter to free space and expose different failure modes such as congestion at chokepoints or poor utilization of occluded regions.

Parameter Optimization
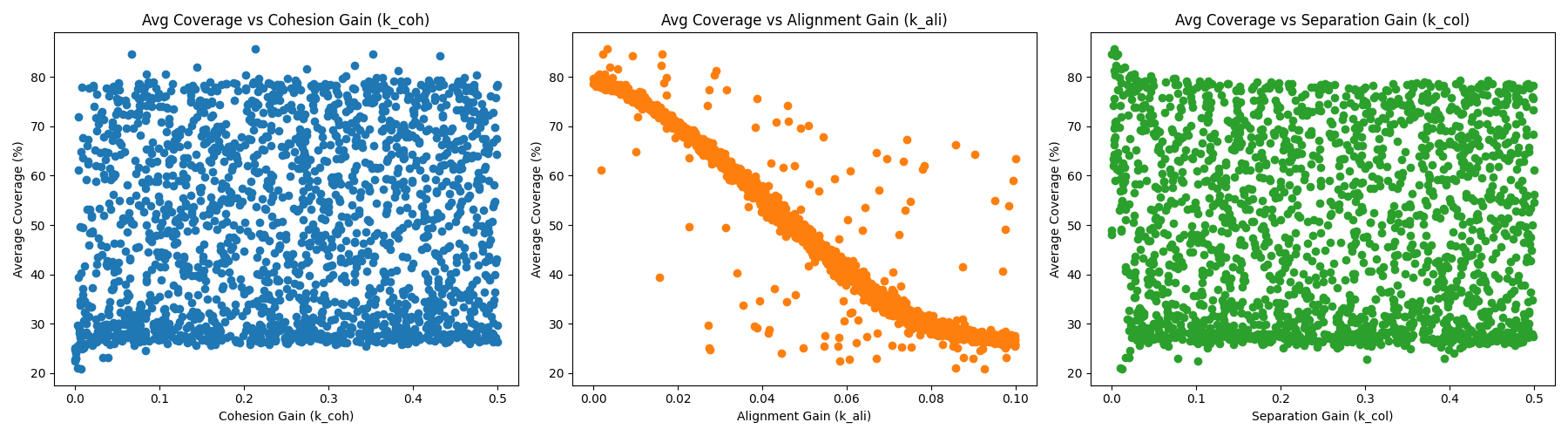
We conducted a random search across 2,000 gain vectors \((k_{\text{sep}}, k_{\text{ali}}, k_{\text{coh}})\), repeated under multiple random seeds, yielding 48,000 simulations in total when scaled across environments and swarm sizes. Early sweeps indicated that large alignment weights consistently degraded coverage, motivating subsequent sweeps with restricted alignment ranges. All other simulation parameters were fixed to isolate the effect of relative gain weighting.
Results
For \(N=50\) and \(N=100\) agents, coverage increased monotonically with swarm size across all environments. In cluttered maps, larger swarms also reduced variance in visitation, overcoming bottlenecks more effectively. Alignment displayed a strong negative correlation with coverage beyond \(k_{\text{ali}} \approx 0.03\), while moderate cohesion and separation improved spatial dispersion without overconstraining motion. In the cafeteria environment with 100 agents, the optimal configuration \((k_{\text{coh}}, k_{\text{ali}}, k_{\text{sep}}) = (0.213, 0.003, 0.003)\) achieved mean coverage of 85.8% across seeds with low CV.
Heatmaps of visitation confirm that low-alignment swarms spread broadly and exploit occluded regions, while high-alignment swarms collapse into rigid flocks that underutilize free space. Corridor scenarios highlight sensitivity to bottlenecks: insufficient separation prevents agents from diffusing into downstream regions, a failure mode mitigated by larger populations.
Discussion
Our results show that local boid rules, when tuned for task performance rather than biological fidelity, provide a lightweight distributed controller for coverage. The prioritized-acceleration formulation prevents pathological superposition of forces and yields interpretable behavior. Optimal coverage emerges in regimes with negligible alignment, moderate cohesion, and moderate separation — effectively encouraging dispersion while preserving group coherency.
The framework remains limited by idealized sensing assumptions and simplified agent dynamics. Noise, occlusion, and heterogeneous capabilities are absent, and controller gains are static rather than adaptive. Nevertheless, large-scale randomized sweeps enabled principled characterization of performance landscapes, which would be infeasible in hardware.