Aerodynamic Analysis of the Boeing B-29 Superfortress
For this project, I examined the aerodynamic characteristics of the Boeing B-29 Superfortress, an aircraft that pushed the boundaries of aeronautical engineering during World War II. Its massive size, advanced pressurized cabin, and sophisticated fire control systems were remarkable achievements for the time. The aerodynamic design of the B-29’s wing played a crucial role in its performance capabilities.
The analysis explored both 2D and 3D effects through a combination of theoretical calculations and computational simulations. Specifications for the plane as a whole were available through various sources, including the National Museum of the United States Air Force and Wikipedia. The B-29’s wingspan is 141.25 feet (43.05 m), with a wing area of 1736 ft² (161.3 m²). The maximum takeoff weight is 133,500 lbf (593,837.37 N), and the cruise speed is 220 mph (98.35 m/s).
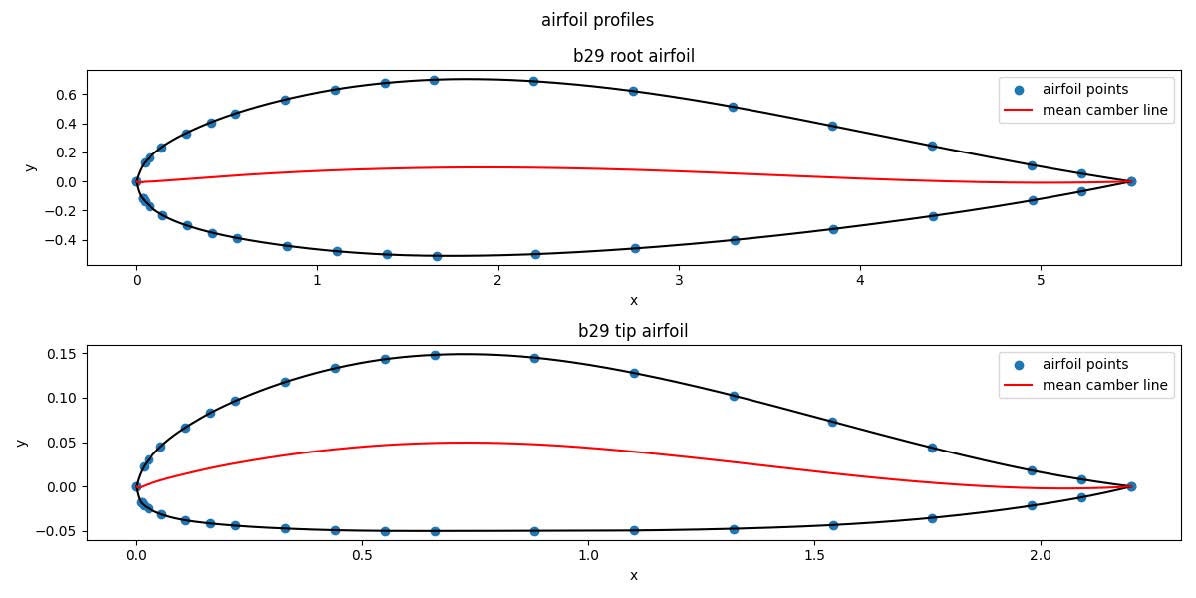
The airfoil profile at the root and tip sections were obtained from Airfoil Tools. However, data for the chord length at either section were unavailable, so I used a three-view image of the B-29 and video analysis to measure the lengths.
- Root Airfoil Chord Length: 18 ft (5.5 m)
- Tip Airfoil Chord Length: 7.22 ft (2.2 m)
Thin Airfoil Theory
Thin airfoil theory provides an analytical approach to determine lift and moment characteristics of cambered airfoils. The vortex-sheet strength \(\gamma(x)\) is calculated from the integral equation:
\[ \frac{1}{2\pi} \int_0^c \frac{\gamma(\xi)}{\xi - x} d\xi = V_\infty \left[ \alpha - \frac{dz}{dx} \right] \]
Rewriting in terms of \(\theta\):
\[ \frac{1}{2\pi} \int_0^\pi \frac{\gamma(\theta)\sin(\theta)}{\cos(\theta)-\cos(\phi)} d\theta = V_\infty \left[ \alpha - \frac{dz}{dx} \right] \]
The vortex-sheet strength \(\gamma(\theta)\) is represented as a Fourier sine series. Using additional manipulations, the section lift coefficient is approximated as:
\[ C_L(\alpha) = 2\pi \left( \alpha + \frac{1}{\pi} \int_0^\pi \frac{dz}{dx} \cos(\phi) d\phi - 2 \right) \]
- The lift-curve slope is approximately \(2\pi\), yielding 6.2831.
- The zero-lift angle of attack is approximately -0.0051 radians (-0.29 degrees).
Estimating Lift Force using Finite Wing Theory
Finite wing theory accounts for the real-world effects of finite wings, such as wingtip vortices and downwash. These effects alter the lift distribution and reduce overall aerodynamic performance compared to idealized infinite wings.
The coefficient of lift for a finite wing is calculated as:
\[ C_L = \frac{2}{V_\infty S} \int_0^\pi \left( \sum_{n=1}^\infty A_n \sin(n\theta) \right) d\theta \]
Finite wing estimates yield lower lift coefficients compared to thin airfoil theory, primarily due to wingtip vortices reducing the effective angle of attack.
Drags (Induced and Viscous)
Induced drag is caused by wingtip vortices, while skin friction drag arises from shear stress due to viscous effects. The induced drag coefficient is calculated as:
\[ C_{D_{induced}} = \frac{C_L^2}{\pi (AR)(1 + \delta)} \]
Skin friction drag is calculated using strip theory and the Blasius formula for turbulent flow:
\[ C_f = \frac{0.027}{\text{Re}_x^{1/7}} \]
The total drag coefficient \(C_D\) is the sum of induced drag and viscous drag.
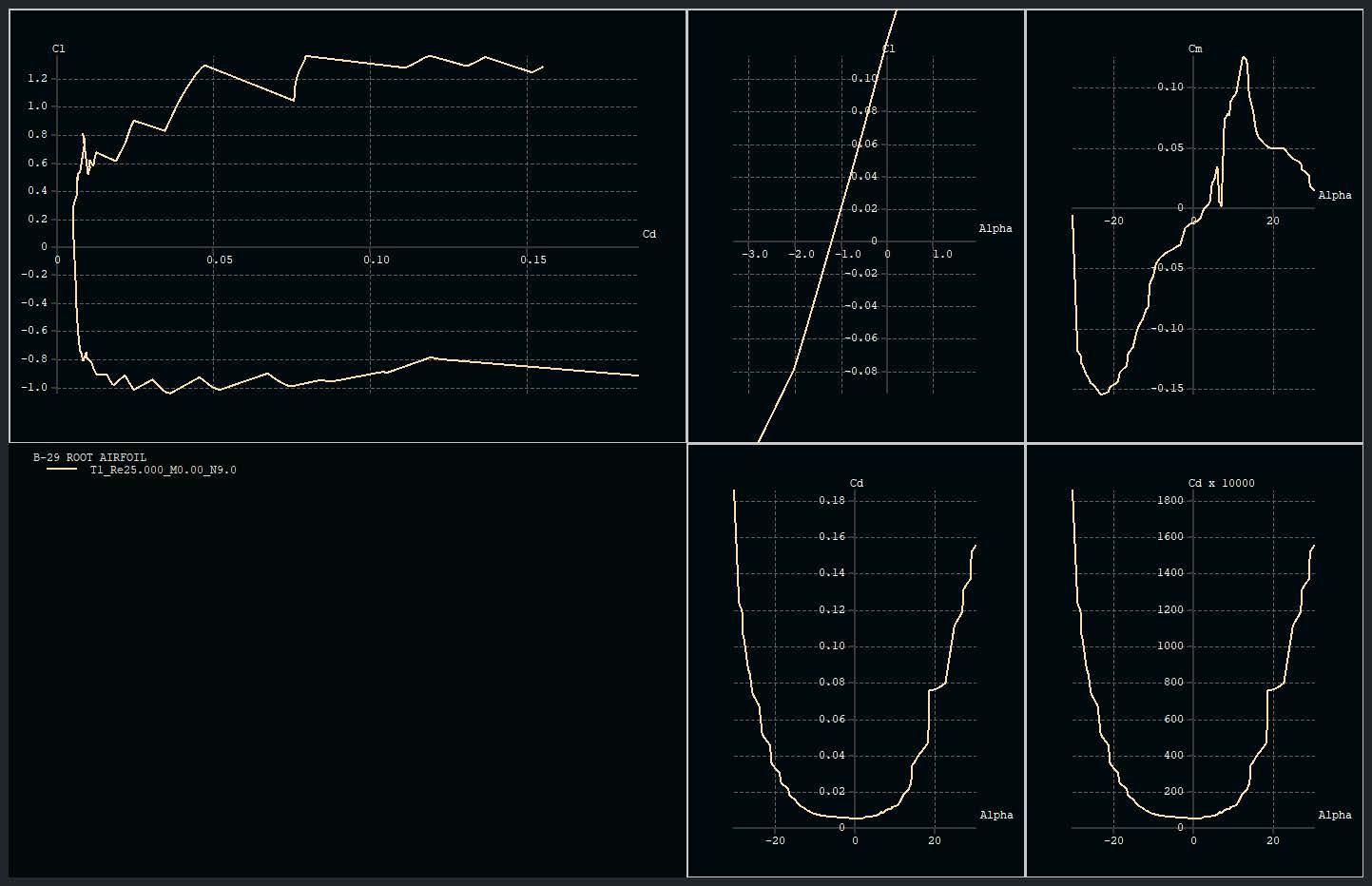
XFLR5 was used to validate the results. The software was able to analyze both airfoils and wings, providing lift and drag polars for the B-29. The zero-lift angle of attack for the root airfoil was larger than predicted by thin airfoil theory, but the results for induced drag were consistent with theoretical predictions.